Quadriláteros

Explicamos o que é um quadrilátero e como esse polígono é classificado. Além disso, quais são suas principais características e alguns exemplos.

O que são quadriláteros?

Quadriláteros são polígonos (figuras geométricas planas) com quatro lados e duas diagonais . Eles são caracterizados por terem quatro vértices e quatro ângulos, e a soma de seus ângulos internos é sempre 360 ​​°. Por exemplo: um quadrado, um trapézio ou um losango.

Essas figuras também são conhecidas como quadrângulos e são usadas em disciplinas como geometria. A palavra quadrilátero deriva do latim, dos termos quadri (quatro) e latus (lados).

Veja também: Teorema de Pitágoras

Características quadrilaterais

Algumas das principais características dos quadriláteros são:

• São polígonos, ou seja, figuras geométricas fechadas e planas formadas por lados e vértices.
• Eles podem ser simples ou complexos e em todos os casos têm quatro lados e quatro vértices.
• Eles podem ter formatos diferentes e sempre têm duas diagonais.
• Eles têm quatro ângulos externos e quatro ângulos internos (que somam 360 °).
• Eles são classificados de acordo com a soma de seus ângulos internos em côncavos e convexos.
• De acordo com o paralelismo de suas faces podem ser: paralelogramos, trapézios ou trapézios.

Elementos quadrilaterais

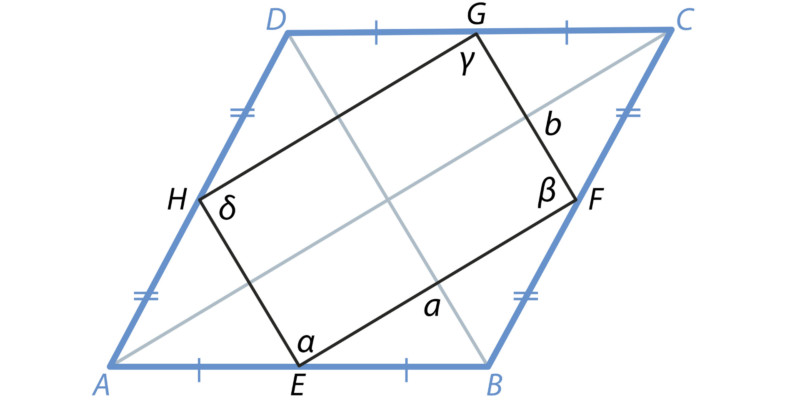
Os quadriláteros são caracterizados por ter os seguintes elementos:

• Lados . São linhas ou segmentos que unem os vértices e que podem ou não ser iguais entre si.
• Vértices . Eles são os pontos de intersecção dos lados. Cada quadrilátero possui quatro vértices.
• Diagonais . Eles são segmentos que conectam vértices opostos.
• Ângulos interiores . Eles são os ângulos visíveis que são determinados pelos lados que os compõem. Os ângulos internos de um quadrilátero somam 360 °.
• Ângulos externos . Eles são os ângulos que são formados com linhas imaginárias (lados) que continuam as linhas do quadrilátero.

Tipos quadriláteros

Os quadriláteros podem ser classificados de acordo com sua forma em quadriláteros complexos e quadriláteros simples.

• Quadriláteros complexos . Eles são aqueles em que dois de seus lados se cruzam.
• Quadriláteros simples . São aqueles em que seus lados não se cruzam e podem ser:
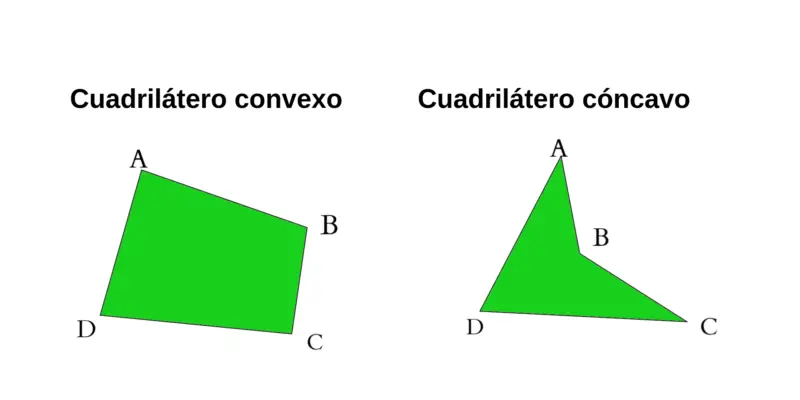
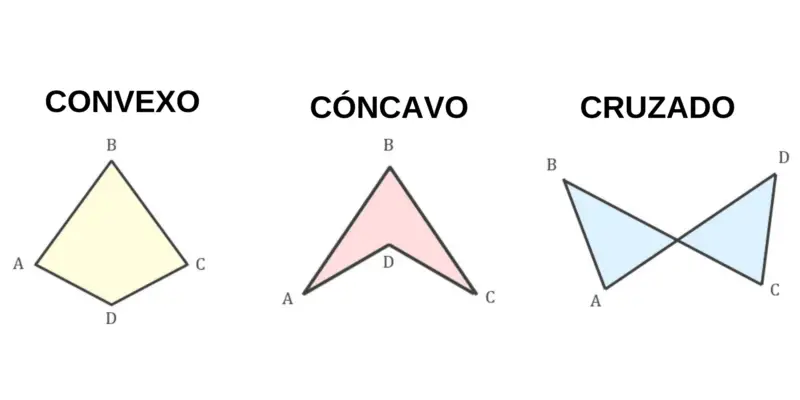
  • Quadriláteros côncavos . Eles são quadriláteros que têm um ângulo que mede mais de 180 °.
  • Quadriláteros convexos . São quadriláteros sem ângulo interno que mede 180 ° ou mais.
  • Quadriláteros cruzados . Eles são quadriláteros que têm lados que se cruzam ou se cruzam.

Quadriláteros convexos podem ser:

1. Paralelogramos

Eles são quadriláteros que têm dois pares de lados paralelos e os lados opostos são idênticos um ao outro. Além disso, os ângulos internos opostos são iguais entre si e as diagonais se cruzam em seu ponto médio. Alguns exemplos são:

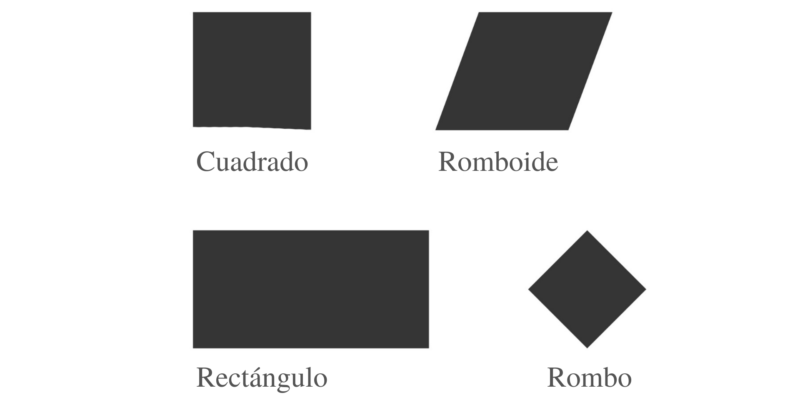
• Romboide . Um quadrilátero que tem quatro lados que não são perpendiculares e os lados opostos são iguais.
• Rombo . Quadrilátero que tem quatro lados iguais, mas que não formam ângulos retos.
• Retângulo . Quadrilátero que tem quatro lados e cada par de lados paralelos tem o mesmo comprimento. Como quadrados, eles têm quatro ângulos retos.
• Square . Quadrilátero com quatro lados iguais e quatro ângulos retos.

1. Trapézio

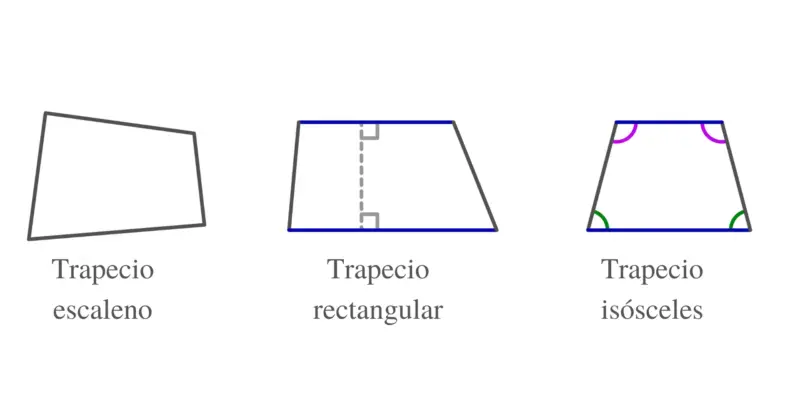
Eles são quadriláteros que possuem dois lados paralelos , que são chamados de base maior e base menor. Os trapézios podem ser:

• Trapézio escaleno . Ele tem seus quatro ângulos internos irregulares.
• Trapézio isósceles . Possui os mesmos lados não paralelos.
• Trapézio retangular . Tem dois ângulos internos que são retos e dois que não são.

Mais em: Trapézio

1. Trapézio

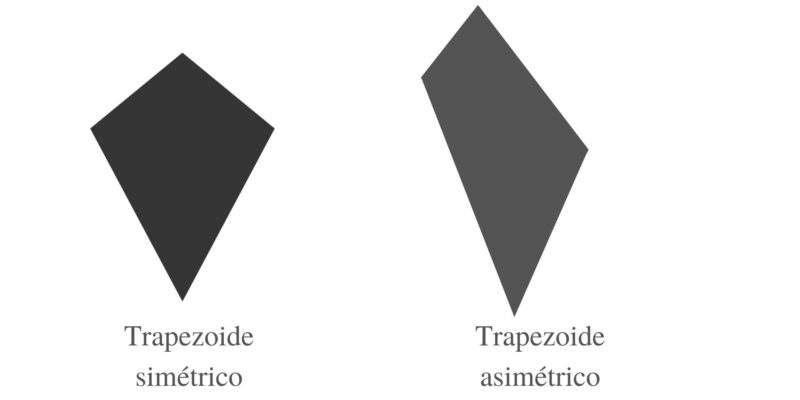
Eles são quadriláteros que não têm nenhum de seus lados paralelos entre si. Eles são divididos em:

• Trapézios simétricos . Eles têm um eixo interno de simetria
• Trapézios assimétricos ou amorfos . Eles não têm um eixo interno de simetria.

Pode ajudá-lo: Vetores