Explicamos o que é o teorema de Pitágoras, como é formulado e explicado. Além disso, quais são suas características, usos e exemplos.
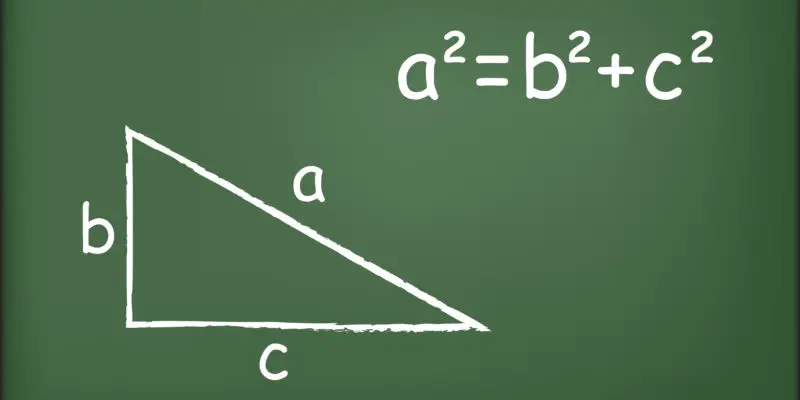
O que é o teorema de Pitágoras?
El Teorema de Pitágoras es un postulado matemático hecho por el filósofo y matemático griego Pitágoras de Salmos (c. 569 – c. 475 a. C.), estudioso de las leyes de la matemática cuyos aportes a la aritmética y la geometría persisten hasta hoy em dia. Este postulado diz que a soma do quadrado das pernas de um triângulo retângulo é sempre igual ao quadrado de sua hipotenusa.
Essa proposição é, sem dúvida, uma das mais conhecidas da história da matemática , e a que apresenta o maior número de provas ao longo do tempo, por meio de métodos diversos e elaborados por diversos filósofos e matemáticos.
Segundo alguns autores , podem ser encontradas até mil provas diferentes , embora 367 tenham sido formalmente catalogadas, pois a prova do teorema era uma exigência durante a Idade Média para se obter o título de Magister Matheseos (“Mestre em Matemática” ) na academia.
Veja também: Vetores
História do Teorema de Pitágoras

Embora a autoria do teorema seja atribuída ao grego Pitágoras , já que sua prova foi de capital importância para os filósofos pitagóricos (discípulos formados em um culto quase religioso da matemática), a verdade é que a origem desse teorema é muito anterior.
Há evidências de seu uso em tabuinhas e papiros babilônios do Egito Antigo , mas nenhum documento que expõe sua relação foi preservado até hoje. Sabe-se que o estudo dos triângulos foi fundamental para muitas das culturas antigas.
Preceitos básicos do Teorema de Pitágoras
Para começar com o teorema de Pitágoras, deve-se entender que as pernas de um triângulo retângulo que formam o ângulo reto (90 °) são chamadas de pernas, e o lado restante e mais longo é chamado de hipotenusa .
Fórmula do Teorema de Pitágoras
O teorema de Pitágoras é formulada como se segue: um 2 + b 2 = c 2 , onde um e b são as pernas de um triângulo rectângulo e onde C é a sua hipotenusa. Desta formulação, três corolários ou formulações subsequentes são derivados, de aplicação prática e verificação algébrica:
- a = √ c 2 – b 2 ( a é igual à raiz quadrada de c ao quadrado menos b ao quadrado)
- b = √b 2 – a 2 ( b é igual à raiz quadrada de c ao quadrado menos a ao quadrado)
- c = √a 2 + b 2 ( c é igual à raiz quadrada de a ao quadrado mais b ao quadrado)
Explicação do Teorema de Pitágoras
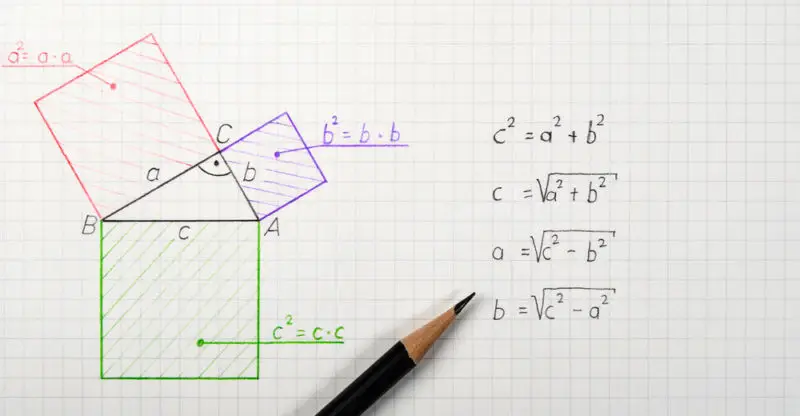
A lógica do teorema de Pitágoras é bastante simples e evidente. Dado um triângulo com lados a, b e c, em que aeb formam um ângulo reto (ou seja, 90 °), é possível calcular o comprimento da hipotenusa adicionando os quadrados das pernas ou, qualquer um dos os lados do triângulo.
Exemplo do Teorema de Pitágoras
Um exemplo simples de aplicação do teorema é o seguinte:
- Dado um triângulo rectângulo cujos pés um e b medida 3 e 4 cm, respectivamente, pode-se calcular a sua hipotenusa C por substituindo-se os valores na fórmula, como se segue:
c 2 = a 2 + b 2
então c 2 = 3 2 + 4 2
e, portanto, c2 = 9 + 16 = 25
e finalmente c = √ 25 = 5
A hipotenusa c tem 5 cm
Provas do Teorema de Pitágoras
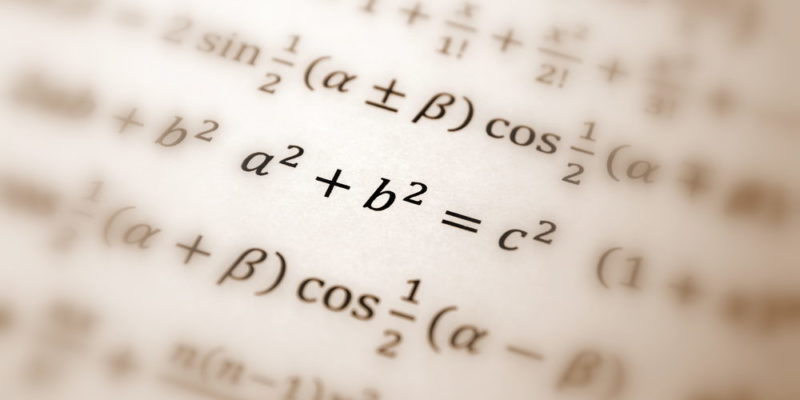
As provas do teorema de Pitágoras são tão variadas quanto numerosas, mas aquelas propostas por Euclides (325-265 aC), Pappus de Alexandria (290-350 aC), Bhaskara II da Índia (114-1185 dC), Leonardo da Vinci (1452-1519 DC) e James Garfield (1831-1881).
Cada um usou diferentes métodos geométricos e aritméticos que, no entanto, sempre levaram à mesma confirmação do teorema.
Prova recíproca do Teorema de Pitágoras
É possível usar este teorema em seu sentido inverso, para verificar se um determinado triângulo está certo (nos casos, por exemplo, onde não pode ser representado graficamente).
Isso é extremamente simples: se em qualquer triângulo for verdade que a soma do quadrado de suas pernas é igual ao quadrado da hipotenusa , então necessariamente as duas primeiras formarão um ângulo reto e >
Aplicações do Teorema de Pitágoras

As aplicações deste teorema são numerosas no campo da engenharia, arquitetura e geometria em geral . Desde os tempos antigos, o estudo do triângulo para fins práticos rendeu frutos tangíveis, como as famosas pirâmides do Egito.
Qualquer situação de cálculo em que um triângulo retângulo esteja presente permitirá a aplicação deste teorema para calcular qualquer um de seus lados.
Importância para outras áreas
Outras áreas da matemática podem usar este teorema para seus cálculos. Por exemplo:
- Geometria analítica plana. Este teorema é usado para encontrar a distância entre pontos em um plano cartesiano.
- Trigonometria. Este teorema é usado para provar a identidade fundamental sen2 a + cos2 a = 1.
Exercícios sobre o Teorema de Pitágoras
Aqui estão dois exercícios a esse respeito:
- Dada a hipotenusa de 20 cm em um triângulo retângulo, do qual uma de suas pernas também tem 5 cm, qual será o comprimento da perna restante?
- Se uma rampa precisa ser feita em um degrau de escada e sabe-se que a altura do degrau é de 30 cm e o comprimento do degrau é de 1 m, quanto deve medir o plano inclinado da rampa?
Continue com: Polígonos